《位似》相似PPT课件

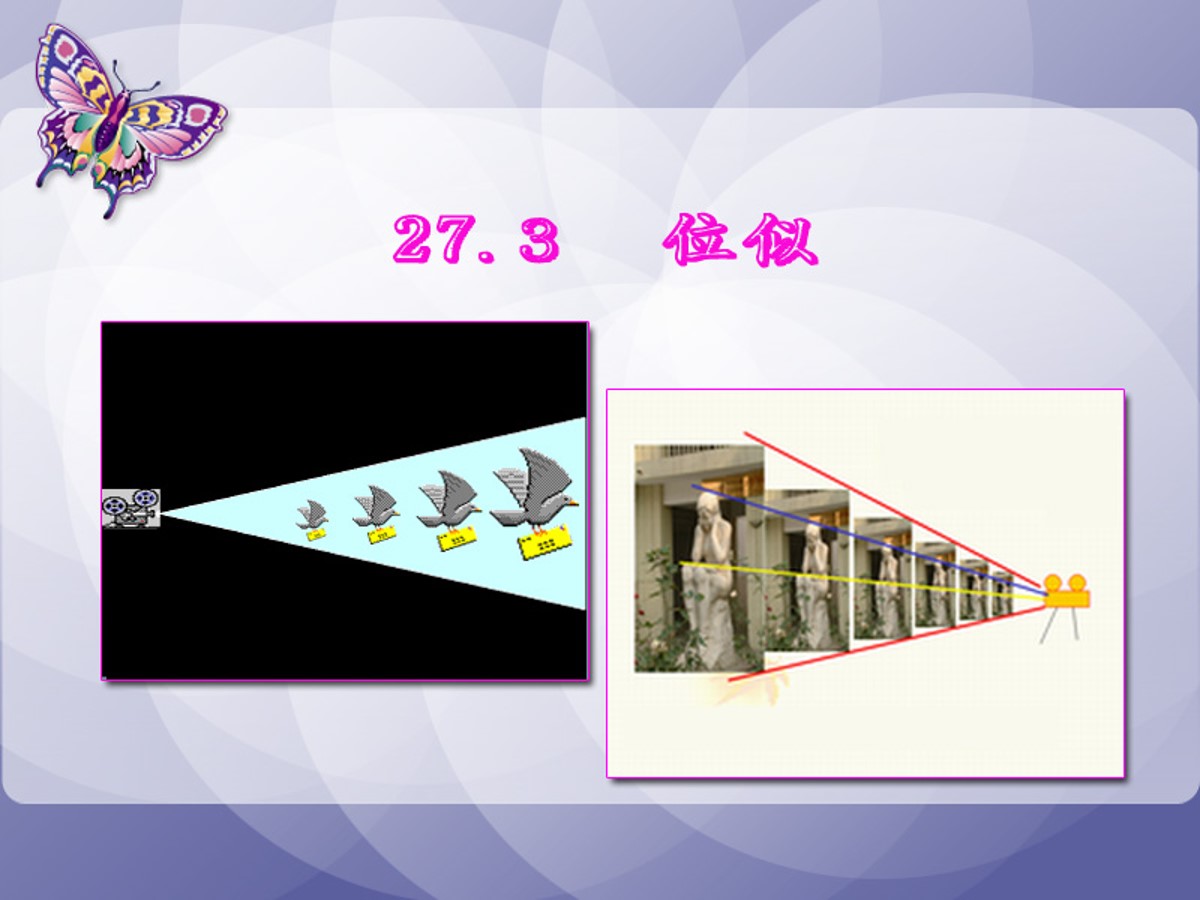
1. 在幻灯机放映图片的过程中，这些图片有什么关系？

2. 幻灯机在哪儿呢？

3.我们能给这种有特殊位置的相似图形一个名称吗？

知识与能力

了解位似图形及其有关概念，了解位似与相似的联系和区别，掌握位似图形的性质。

掌握位似图形的画法，能够利用作位似图形的方法将一个图形放大或缩小。

掌握直角坐标系中图形的位似变化与对应点坐标变化的规律。

过程与方法

经历位似图形性质的探索过程，进一步发展学生的探究、交流能力、以及动手、动脑、手脑和谐一致的习惯。

情感态度与价值观

利用图形的位似解决一些简单的实际问题，并在此过程中培养学生的数学应用意识，进一步培养学生动手操作的良好习惯。

发展学生的合情推理能力和初步的逻辑推理能力。

... ... ...

教学重难点

位似图形的有关概念、性质与作图。

利用位似将一个图形放大或缩小。

直角坐标系中图形的位似变化与对应点坐标的关系。

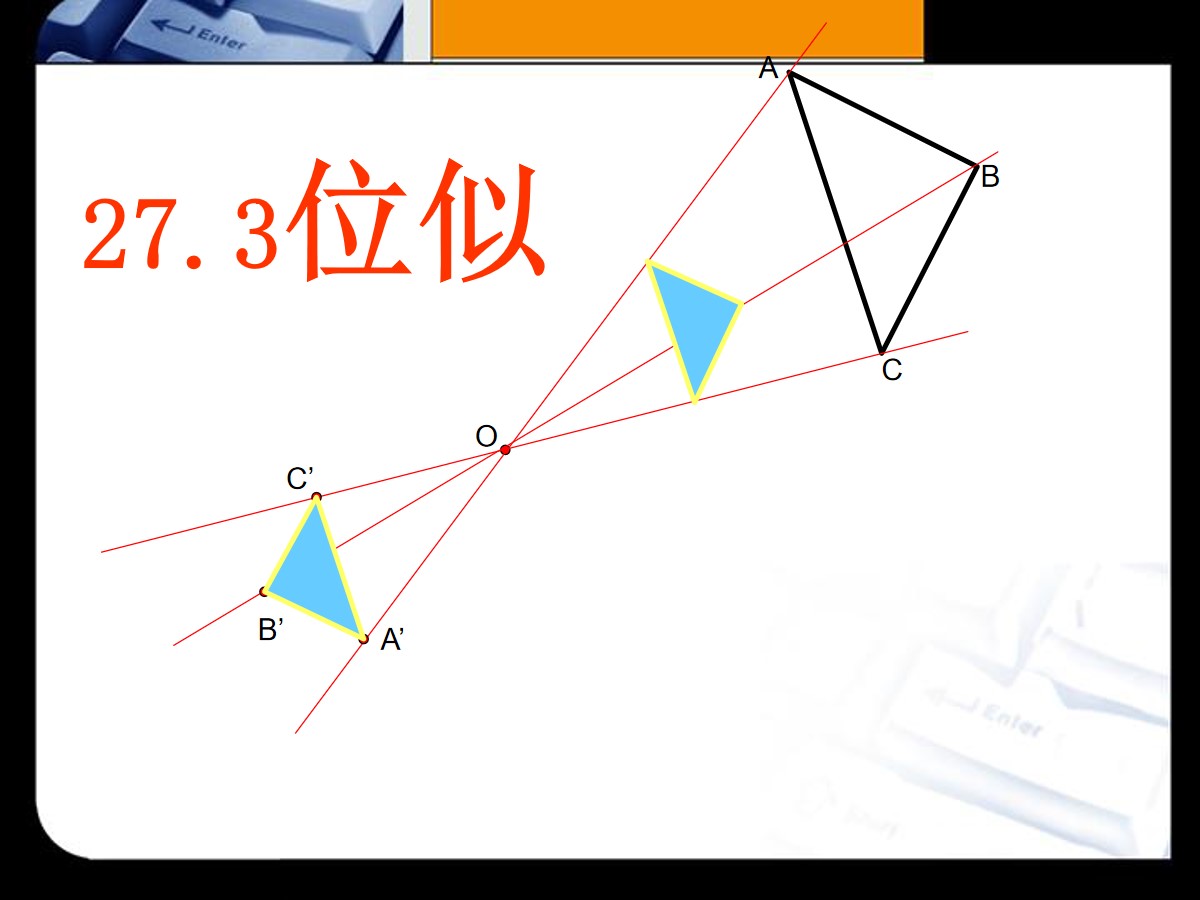
不仅相似，而且对应顶点的连线相交于一点，对应边互相平行，像这样的两个图形叫做位似图形（homothetic figures），这个点叫做位似中心，这时的相似比又称为位似比。

位似是一种具有位置关系的相似。

位似图形是相似图形的特殊情形。

位似图形必定是相似图形，而相似图形不一定是位似图形。

两个位似图形的位似中心只有一个。

两个位似图形可能位于位似中心的两侧，也可能位于位似中心的一侧。

... ... ...

位似图形的性质

对应点与位似中心共线。

不经过位似中心的对应边平行。

位似图形上任意一对应点到位似中心的距离之比等于位似比。

位似变换的步骤 

①确定位似中心，位似中心的位置可随意选择；

②确定原图形的关键点，如四边形有四个关键点，即它的四个顶点；

③确定位似比，根据位似比的取值，可以判断是将一个图形放大还是缩小；

④符合要求的图形不唯一，因为所作的图形与所确定的位似中心的位置有关，并且同一个位似中心的两侧各有一个符合要求的图形。

... ... ...

位似多边形

如果两个图形不仅相似，而且每组对应顶点所在的直线都经过同一个点，那么这样的两个图形叫做位似图形，这个点叫做位似中心，这时的相似比又称为位似比。

在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或-k，则像上的对应点的坐标为（kx，ky）或（－kx，－ky）。

1. 位似图形、位似中心、位似比：

如果两个图形不仅形状相同,而且每组对应顶点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形。

这个点叫做位似中心。

这时的相似比又称为位似比.

2. 位似图形的性质：

位似图形上的任意一对对应点到位似中心的距离之比等于位似比。

以坐标原点为位似中心的位似变换有以下性质：若原图形上点的坐标为（x，y），与原图形的位似比为k，则像上的对应点的坐标为（kx，ky）或（Dkx，Dky）。

3. 位似图形的画法：

画出基本图形。     

选取位似中心。

根据条件确定对应点，并描出对应点。

顺次连结各对应点，所成的图形就是所求的图形。

... ... ...

1. 判断下列各对图形哪些是位似图形，哪些不是. 

（1）五边形ABCDE与五边形A′B′C′D′E′ 

（2）正方形ABCD与正方A′B′C′D′

（3）等边三角形ABC与等边三角形A′B′C′

2. 下面的说法对吗?为什么?

（1）分别在△ABC的边AB,AC上取点D,E,使DE∥BC,那么△ADE是△ABC缩小后的图形。

（2）分别在△ABC的边AB,AC的延长线上取点D,E,使DE∥BC,那么△ADE是△ABC放大后的图形。

（3）分别在△ABC的边AB,AC的反向延长线上取点D,E,使DE∥BC,那么△ADE是△ABC缩小后的图形。

... ... ...

《位似图形》PPT课件 观察与思考 下列图形中，每个图中的四边形ABCD和四边形ABCD都是相似图形.分别观察这五个图，你发现每个图中的两个四边形各对应点的连线有什么特征？ 明晰新知 如..

《相似多边形和图形的位似》PPT课件2 1．两个________多边形，如果它们__________________相交于一点，我们就把这两个图形叫做位似图形，这个交点叫做________，这时的相似比又叫做__..

《相似多边形和图形的位似》PPT课件 1．对应角________、对应边________的两个多边形叫做________． 2．两个相似多边形的周长比等于它们的__________；相似多边形面积的比等于它们的_..