《图形的相似》相似PPT课件2

知识与能力

感知相似图形在现实中的应用。

认识形状相同的图形。

了解相似图形的基本内涵。

过程与方法

通过观察、操作，了解相似图形的过程。

进一步了解相似形在实际生活中的应用。

掌握简单的画图方法，在动手操作中认识 相似图形。

... ... ...

两个图形的形状 ________，但图形的大小位置 __________，这样的图形叫做相似图形。

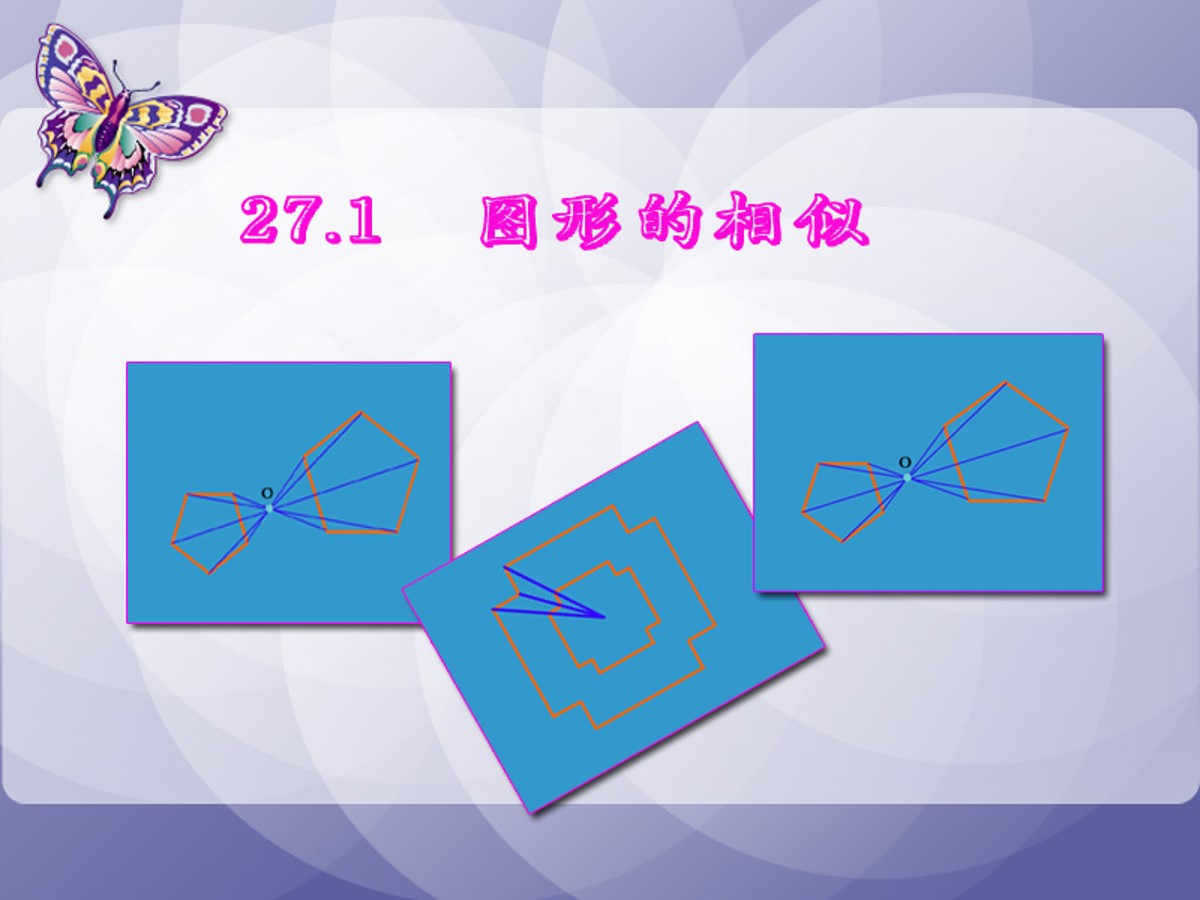
相似图形的关系

两个图形相似，其中一个图形可以看作由另一个图形放大或缩小得到。

由在同一平面且不在同一直线上的多条线段首尾顺次连结且不相交所组成的图形叫做多边形。

相似多边形

根据相似多边形的特征，给相似多边形下定义。

各对应角相等、各对应边成比例的多边形叫做相似多边形.

... ... ...

相似多边形的性质

相似多边形对应高的比、对应角平分线的比、对应中线的比、对应周长的比都等于相似比。

相似多边形对应对角线的比等于相似比。

相似多边形对应三角形相似，且相似比等于相似多边形的相似比。

相似多边形面积的比等于相似比的平方。

相似多边形对应三角形面积的比等于相似多边形的相似比的平方。

... ... ...

题型1  判断两个多边形是否相似

解: ∵ 正方形，菱形的四条边都相等. 

∴ 它们的对应边成比例，k =  3 : 4.

∵ 正方形的四个内角均为直角，而菱形的内角有钝角有锐角.

∴ 它们的对应角不相等.

∴ 这一组图形不相似.

一块长 3m，宽1.5m的矩形黑板，镶其外围的木质边宽7.5cm。边框内外边缘所组成的矩形相似吗?为什么?

解: ∵ 矩形的每个内角都等于90o.

∴ ∠A =∠E = 90°，∠B =∠F  = 90°   

∠C =∠G = 90°，∠D =∠H = 90°

∴ 它们的对应角相等.

∵ EH:AD=300:(300+2×7.5)=20/21.

EF:AB =150:(150+2×7.5)=10/11.

∴ EH:AD≠EF:AB.

∴ 它们的对应边不成比例.

∴ 矩形ABCD和矩形EFGH不相似.

... ... ...

1. 判断：

（1）任意两个矩形都是相似图形（      ） 

（2）任意两个圆形是相似图形（      ） 

（3）对应角相等的两个四边形是相似多边形（      ）

（4）两个正五边形是相似多边形（      ）

（5）两个全等三角形是相似多边形（      ） 

（6）两菱形是相似多边形（      ） 

（7）两个相似多边形，对应边成比例（      ） 

2. 五边形ABCDE相似于五边形A′B′C′D′E′，它们的相似比为1 : 3，

（1）若∠D＝135°，则∠D′= ______。 

（2）若A′B′=15cm，则AB= ______。

3.  一个多边形的边长分别是2、3、4、5、6，另一个和它相似的多边形的最短边长为6，则这个多边形的最长边为______ 。  

《图形的相似》相似PPT课件3 学习目标 1.从生活中形状相同的图形的实例中认识图形的相似，理解相似图形的概念； 2.理解相似图形的性质和判定. 相似多边形的性质: 相似多边形对应角相..

《图形的相似》相似PPT课件 知识点、考点回顾： 一、比例： 1、比例：如果a:b与c:d的比值相等，我们就说这四个数abcd成比例，写成比例式a:b=c:d。 2、第四比例项：若a/b=c/d，则d叫a..

《图形的位似》图形的相似PPT课件3 一．位似图形的概念 如果两个图形不仅相似，而且每组对应顶点所在的直线都经过同一点，对应边互相平行（或共线）那么这样的两个图形叫做位似图形这..